
목차
1. 이변량 분석 : 수치 → 수치
2. 이변량 분석 : 범주 → 수치
3. 평균과 분산에 대하여
내일 AICE. 급하다. 빠르게 가자.
이변량 분석 : 수치 → 수치
지난 시간에 가설에 대해 배웠다.
이변량 분석은 결국 x가 y에 영향을 끼치는지를 보는 가설 검정 과정이라고 할 수 있겠지.
데이터사이언스가 늘 그렇듯이 자료의 타입(범주형/수치형)에 따라 분석 방법이 다르다.
그중 첫번째. x도 수치고 y도 수치인 경우를 보자.
이변량 분석은 일반적으로 시각화와 수치화를 통해 진행된다.
| 수치 → 수치 이변량 분석 방법론 | |
| 시각화 | scatterplot, regplot, jointplot, pairplot, heatmap |
| 수치화 | 상관계수, 상관분석 |
- 시각화
1. scatterplot
산점도. 하나의 row 정보를 그래프 위에서 점으로 나타내 분포를 시각화한다.
plt.figure(figsize=(4, 4))
sns.scatterplot(x='var', y='target', data = data)
plt.grid()
plt.tight_layout()
plt.show()
sns 바탕으로 그래프 그릴 때 일반적으로 쓰는 형식.
figsize는 적절히 조정해 주면 되고, var나 target, data는 변수로 선언해 두면 편하다.
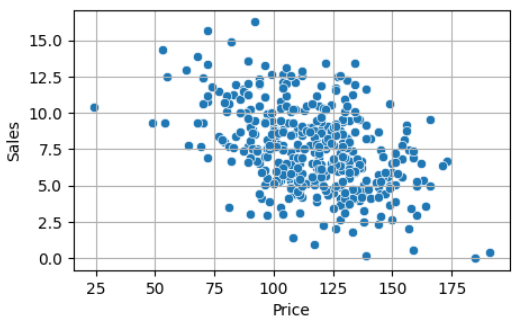
대충 이렇게 생긴 게 나온다.
sns 그래프가 대체로 그렇듯이, hue 옵션을 통해 범주값 별로 볼 수도 있다.
plt.figure(figsize=(4, 4))
sns.scatterplot(x='var', y='target', data = data, hue='col')
plt.grid()
plt.tight_layout()
plt.show()
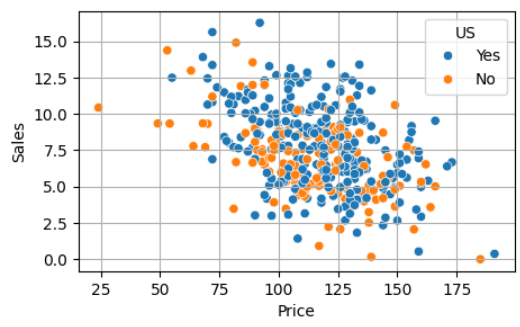
이런 식으로 가능.
sns는 palette 옵션으로 색을 줄 수도 있는데, 미프때 메시지 뜨는 거 보니까 조만간 막힌다고 하더라. 아쉽
. regplot, jointplot, pairplot
산점도 기반에 다른 옵션이 추가된 것들이다.
코드는 위와 똑같은 상태에서 scatter만 다른 걸로 바꿔 주면 된다. seaborn 만만세.
regplot은 추세선(회귀선, regressor line)을 그려준다. 다만 추세가 없어도 그리니 조심.

jointplot은 데이터 밀도를 나타내는 히스토그램을 붙여준다.

pairplot은 데이터프레임에 포함된 수치형 함수들을 죄다 모아서 산점도를 그려 준다.
좀 멋있긴 한데 오래 걸린다. 분석단계 처음에 한 번 보고 가기 좋은 듯.
sns.pairplot(data)
plt.tight_layout()
plt.show()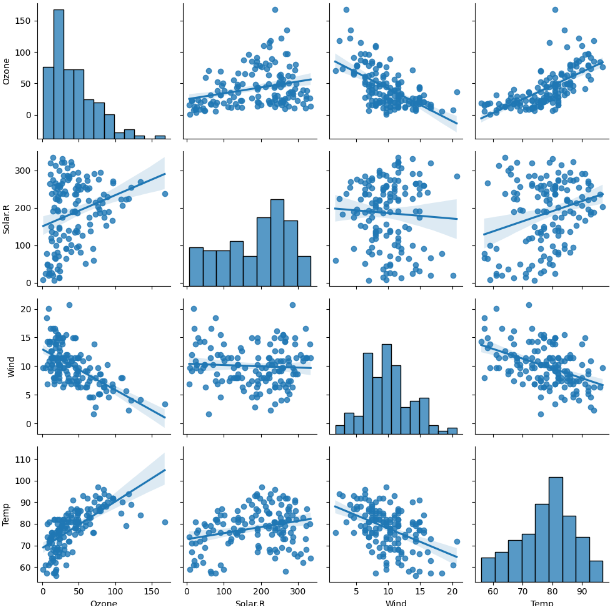
- 수치화
수치화는 단계를 거친다.
관계를 수치화하여 상관계수 도출 → 상관계수가 유의미한지 상관분석 실시
1. 상관계수 도출
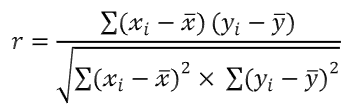
상관계수란 두 수치형 변수간의 관계를 수치로 나타낸 것이다.
-1에서 1사이의 값으로, 절댓값이 1에 가까울수록 강한 상관관계, 0에 가까울수록 약한 상관관계다.
강사님께서 제시해 주신 통상적 기준은
0.5 이상 : 강한 상관관계
0.2 이상 : 중간 정도의 상관관계
0.1 이상 : 약한 상관관계
0.1 미만 : 상관관계가 거의 없음
이 되시겠다.
상관계수를 도출하는 위의 저 식을 코드로 구현하는 건 너무 힘든 일이기에,
pandas에는 데이터프레임에서 직통으로 상관계수를 구해 주는 함수가 있다.
그것은 바로 corr()
df.corr()
캬 코드 단순한 거 봐라. 마음에 든다.
corr()은 해당 데이터프레임의 수치형 데이터들의 모든 상관관계를 matrix 형태로 반환한다.

이렇게. 대각선은 자기 자신과의 상관관계니 완전 일치(1)가 나오고,
그 주대각을 기준으로 위든 아래든 보면 된다.
참고로 corr()을 바탕으로 시각화하는 방법도 있다.
그건 바로 heatmap().
plt.figure(figsize = (8, 8))
sns.heatmap(air.corr(),
annot = True, # 숫자(상관계수) 표기 여부
fmt = '.3f', # 숫자 포멧 : 소수점 3자리까지 표기
cmap = 'RdYlBu_r', # 칼라맵
vmin = -1, vmax = 1) # 값의 최소, 최대값
plt.show()

2. 상관분석
상관계수가 도출되었다곤 하나, 그것이 유의미한지 검정을 진행해야 한다.
사전학슴에서 이 유의성 검정에 사용하는 것으로 피어슨(Pearson) 계수를 배웠었다.
이젠 그걸 써야 한다.
피어슨 계수를 포함한 대부분의 검정 계산은 scipy.stats 모듈을 사용한다.
import scipy.stats as spst
spst.pearsonr(air['var'], air['target']) # 피어슨r 계수 측정
scipy.stats 이니 spst로 선언한다.
이따 범주 → 수치 분석에서도 사용될 예정.
이렇게 시행하면
(0.6833717861490115, 2.197769800200214e-22)
↑ 요런 형태의 튜플을 반환한다.
0번 인덱스가 상관계수, 1번 인덱스가 p-value이다.
(즉, corr() 말고도 spst.pearsonr()로도 상관계수가 구해진다.)
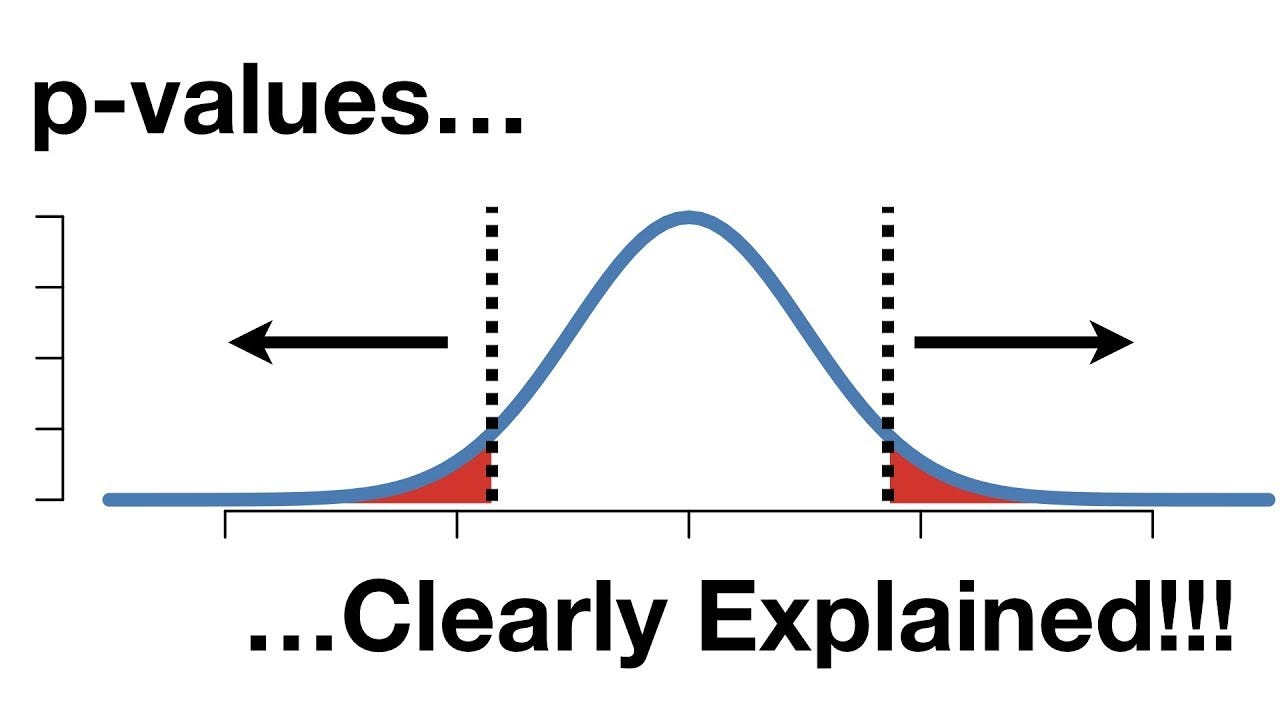
P-value는 잠시 후에 자세히 설명하고,
지금은 P-vlaue가 0.05 미만인 것이 관계가 있음. 즉 대립가설 채택의 조건임을 기억해두자.
여튼 이렇게 상관계수와 상관분석을 통해 이변량 수치 데이터의 관계성을 분석해 볼 수 있다.
여기서 주의사항. 상관계수는 선형 관계만 나타낼 수 있다.
이변량 분석 : 범주 → 수치
이번엔 x가 범주고 y가 수치인 경우이다.
원리가 길고 복잡하기에, 일단 방법론만 빠르게 털고 원리는 뒤에서 다루고자 한다.
| 범주 → 수치 이변량 분석 방법론 | |
| 시각화 | barplot을 통한 평균비교 |
| 수치화 | t-test : 범주요소가 2개일 때 ANOVA : 범주요소가 3개 이상일 때 |
- 시각화
barplot
믿음과 신뢰의 막대그래프.
seaborn의 barplot은 estimator 파라미터 기본값이 mean이라서 대부분 설정이 필요 없다. 개꿀이다.
sns.barplot(x="var", y="target", data=data)
plt.tight_layout()
plt.grid()
plt.show()
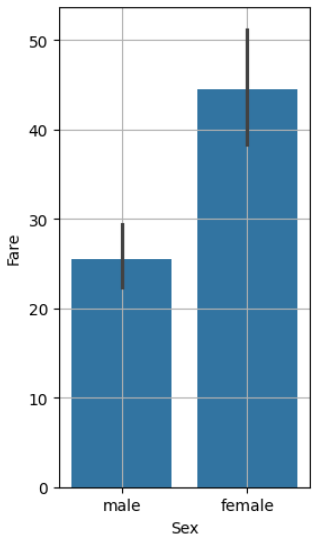
저 양초 심지(?)같은 부분은 이후에 소개할 95% 신뢰구간을 나타낸다.
두 평균값의 차이가 크고 신뢰 구간이 겹치지 않을 때 대립 가설이 맞다고 본다.
이 경우는 딱 봐도 대립가설이 채택될 각.
- 수치화
범주형 컬럼도 두 종류가 있다.
범주가 두 개인 것(성별, 유무, 여부 등등),
그리고 범주가 셋 이상인 것(구간, 학년, 세대, 지역 등등)
이에 따라 수치화 방법이 바뀐다.
1. 범주가 두 개일 때 : T - Test 이모티콘 같아서 귀엽다.
원리는 냅두고 코드부터.
위에서도 봤던 scipy.stats에 있는 함수 ttest()를 쓴다.
# var 컬럼을 두 그룹으로 나누어 저장
g1 = df.loc[df['Var']==0, 'Target'] # 열에 Target 컬럼 꼭 지정
g2 = df.loc[df['Var']==1, 'Target']
# 2) t-test
spst.ttest_ind(g1, g2) # 독립 표본(independent) 검정
컬럼에 속한 범주들을 변수로 선언해 주는게 중요하다.
잊지 말자. 캡슐화.
당연히, loc의 열 인자로 target을 주지 않으면 에러가 뜬다.
결과로
Ttest_indResult(statistic=2.06668694625381, pvalue=0.03912465401348249)
이런 튜플이 반환된다.
0번 인덱스는 t 통계량으로, 절댓값이 2보다 크면 상관관계가 있다고 본다.
1번 인덱스는 p-value로, 0.05보다 작으면 상관관계가 있다고 본다.
2. 범주가 셋 이상일 때 : 분산 분석 ANOVA(ANalysis Of Variance)
1과 원리가 같다. 범주들 변수화하고, spst 함수에 냅다 집어넣기.
이번엔 f 통계량이 필요하므로, 다른 함수인 f_oneway()를 쓴다.
# 그룹별 저장
P_1 = df.loc[df['var'] == 1, 'Target']
P_2 = df.loc[df['var'] == 2, 'Target']
P_3 = df.loc[df['var'] == 3, 'Target']
# 2) 분산분석
spst.f_oneway(P_1, P_2, P_3)
반환 결과도 얼추 비슷하다.
F_onewayResult(statistic=57.443484340676214, pvalue=7.487984171959904e-24)
0번 인덱스는 f 통계량으로, 2~3보다 크면 상관관계가 있다고 본다.
1번 인덱스는 p-value로, 0.05보다 작으면 상관관계가 있다고 본다.
단, ANOVA는 분산 바탕의 비교로 그룹 간의 차이(분산)에 대해서만 알려 준다.
데이터 분석에서는 이정도만 해도 된다고는 하나, 사후분석으로 그룹 내 분산을 보기도 한다.
평균과 분산
- 평균 말고 분산도 필요한 이유.
일반적으로 범주를 바탕으로 수치와의 상관관계를 알려면?
위의 barplot처럼 평균을 비교하면 된다.
반(범주)이 점수(수치)에 영향을 미치는지 봤을 때,
A반과 B반 중에 평균이 높은 반이 더 잘하는 반이겠지.
그런데 이번엔 반이 100개라고 해 보자.
A반이 B반보다 높다고 공부 잘 하는 반인가? 그건 모른다.
그럼 어떻게 해야 공부 잘 하는 반인가?
100개 반의 평균에서 얼마나 떨어져 있는지(편차)를 보면 되겠지.
따라서 우리는 데이터의 가치를 매기기 위해,
평균과 편차를 구한다.

편차에 대한 문과적 해석그래 나 문과다편차는 A반 하나에만 국한된 값이다.
A반이 평균으로부터 많이 멀다 해도,
A반과 같은 위치에 분포한 반이 많으면
A반은 잘 하는 반이라고 하기 힘들다.
따라서 우리는 데이터의 모든 요소들이 갖는 편차를 알아야 한다.
편차를 다 합하면 되겠지?
근데 대칭분포의 편차를 다 합치면 0이 나온다.
잘 친 반 편차는 +x 고 못 친 반 편차는 -x니까.
저놈의 마이너스를 없애 주려면 절댓값을 씌우거나 제곱을 하면 된다.
계산하기에 절댓값 함수는 불편하다(x=0에서 미분이 안 된다.)
그래서 모든 편차에 제곱을 취해서 합하면,
이제 각 값들이 평균에서 떨어진 수준을 알 수 있다.
이것을 분산(Variance)이라고 한다.
근데 사실 분산은 애들이 얼마나 퍼졌는지를 보여주지,
A반과 다른반이 '정확히' 얼마큼 떨어졌는지 알려주진 않는다.(근데 데이터 분석에서는 분산만 있어도 되는듯....?)
왜? 아까 제곱했거든.
그래서 제곱을 풀어준다. 루트 씌워서.
그게 바로 표준편차다.
표준편차가 작단 건 평균에 가까운 애들이 많단거고,
표준편차가 크단 건 평균에서 먼 애들이 많단거다.
A가 평균에서 먼데 표준편차가 작으면 잘 하는 거고
A가 평균에서 먼데 표준편차가 크면 그정도로 잘 하는 건 아니다.
이제 우린 드디어 통계의 두 도구, 평균과 표준편차를 쓸 수 있다.
- 데이터 사이언스 측면의 평균과 분산
본격줄글로 수학공부하기
자, 그럼 이것들이 어떻게 쓰이는 지 보자.
데이터 과잉인 이 시대에 전수조사란 너무도 힘들기에,
우리는 일부 데이터(표본집단)으로 전체 데이터(모집단)을 파악하려 한다.
표본은 우리 손에 있는 데이터니까, 이리저리 주물러서
평균과 분산(표준편차)를 구할 수 있다.
이것들을 지금부터 표본평균과 표본분산이라고 하자.
표본평균은 모집단의 평균(모평균, μ)을 대표할 수 있을까?
가깝긴 하겠지만, 사실 오차가 있을 수밖에 없다.
분하다. 한번 더 뽑아 보자.(모집단은 너무 커서 모평균을 구할 수 없다.)
표본평균이 이전의 표본과는 다르게 나온다. 표본을 새로 뽑았으니 당연하다.
다시 평균을 뽑는다.
2트째라고 모평균에 더 가까울까? 그럴 리가!

그런데 이 짓을 수십 번 반복하면 할수록 신기한 일이 생긴다.
표본평균을 하도 많이 뽑아서 걔네들의 분포를 봤더니, 정규분포 모양이 아닌가?
그 가운데가 표본평균들의 평균이겠지? 근데 이게 모평균에 근사하는게 아닌가?.
(이걸 중심극한정리라고 한다.)
와 축하해라. 드디어 모평균에 근사한 값을 구했다.
- 표준오차와 95% 신뢰구간
하지만 인간이란 상당한 변태다. 이걸로는 만족하지 못한다.
정확한 모평균 지점을 찍지 못한다면,
적어도 오차범위라도 펼쳐서 모평균이 있을 수 있는 범위라도 지정하겠다.
그 이름하야 표준오차.
자, 이쯤에서 표준편차의 지극히 문과적인 의미를 보고 가자.
데이터들이 평균에서 얼마나 떨어졌는지를 표현한 것
우리가 구하려는 것은 뭔가? 모평균의 위치,
정확히는 표본평균들이 모평균에서 얼마나 떨어졌는지 아닌가?
그렇다. 사실 표준오차는 표준편차다. 모평균에 대한 표본평균들의 표준편차.
표본평균 무한 개의 평균은 모평균에 수렴하므로, 이런 계산이 가능하다.(중심극한정리)
물론 실제로는 표본이 무한 개가 아니기 때문에,
이렇게 표준오차를 펼쳐도 모분산이 빗나가기도 한다 ㅋㅅㅋ
따라서 이 오차로부터 얻은 구간을 '95% 신뢰구간' 이라고 한다.
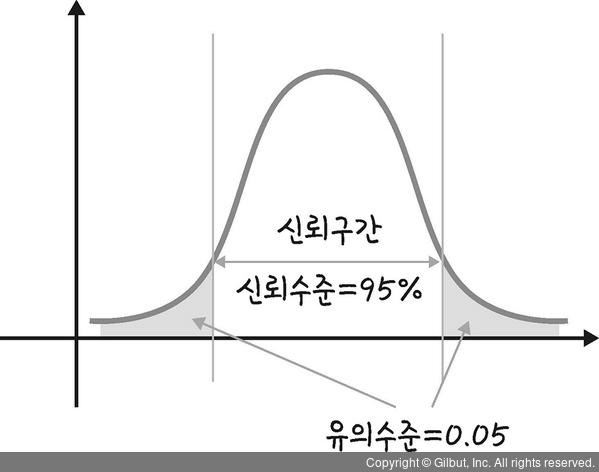
이게 무슨 뜻인고 하니...
우리의 타겟(모평균)은 표본평균들의 평균과 표준오차로 구한 범위(신뢰범위) 안에 있을 확률이 높다.
그 확률을 95%가 되도록 계산하는 것이 국룰인가 보더라.
95%가 되게 계산하기?
신뢰구간을 구할 때의 식을 풀어 쓰면 다음과 같다.
<신뢰구간>
표본평균들의 평균 - (상수*표준오차) ~ 표본평균들의 평균 + (상수*표준오차)
뭐, 식을 외울 필요는 없고...
식에 상수가 들어간다는게 포인트다.(z-score라고 한다.)
저 상수의 정체는,
표준정규분포에서 n% 위치에 매칭된 값이라고 보면 된다.
그 유명한 표준정규분포표에 다 구해져 있다.
표준정규분포표님에게 물어보자.
Q: 신뢰구간이 95% 넓이가 되게 만드는 상수는?
A: 1.96
따라서 표준오차에 1.96을 곱한 후, 표본평균들의 평균으로부터 그만큼 펼치면
그게 95% 신뢰구간이다.

- 그래서 이제 뭐함?
이렇게 95% 신뢰 구간을 구했다면, 그 바깥 범위의 넓이를 p-value라고 한다.
95% 구간 바깥이니까 5% 범위. 정규분포의 넓이는 1이므로...
p-value의 기준은 0.05이다.
이 p-value는 통계적으로 귀무가설이 참일 때 지금처럼 극단적인 데이터를 얻을 확률의 의미로 쓰인다.
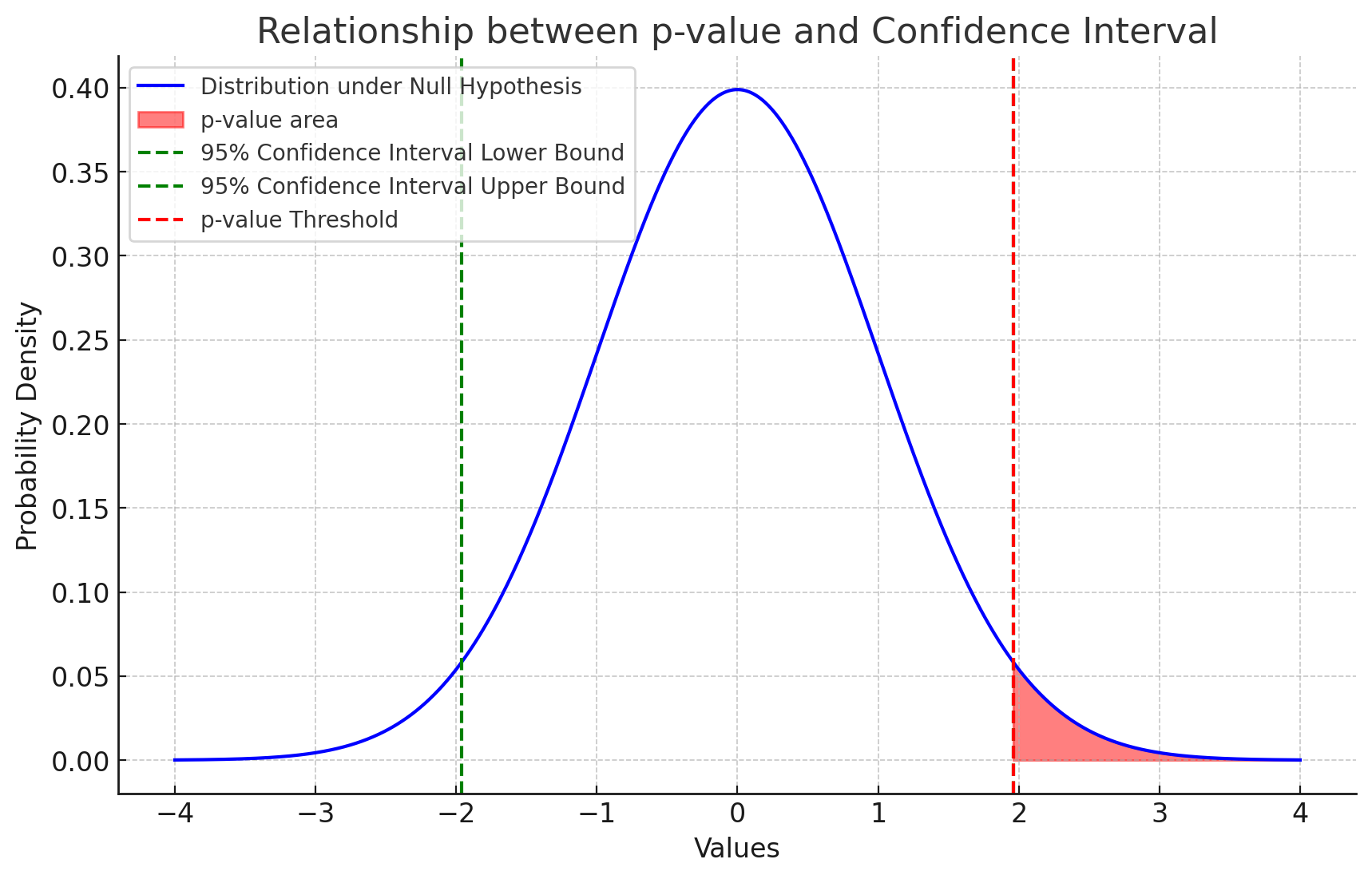
다시말해, 우리가 집어넣은 데이터가 저 붉은 영역 안에 있다면( = p-value가 0.05보다 작다면)
귀무가설이 참일 확률이 상당히 낮단 소리.
이것을 귀무가설을 기각하고 대립가설을 채택(x는 y와 관련이 있다.)하는 근거가 된다.