
목차
1. 이변량 분석 : 범주 → 범주
2. 이변량 분석 : 숫자 → 범주
1차 미프도 잘 끝나고, AICE Associate도 그럭저럭 쳤고!
바쁘던 저번주가 끝나자마자 코딩마스터스 마감과 2차 미프가 스멀스멀 다가오는 이번 주.
주말도 에이블 기자단 활동하랴, DX 10반 소식지 만들랴 정신 없이 지나갔다.
마지막 제자들 수능이랑 면접도 얼마 안 남았고 말이지 ㅎㅎ
진짜 힘내자. 10월의 나.
그래도 잡념이 잘 안 든다는 점에서 이정도 바쁜 게 딱 좋은 걸지도 모르겠다.
그럼 데이터 분석 마지막 수업이었던 오늘도,
복습 드가자잇
이변량 분석 : 범주 → 범주
| 범주 → 범주 이변량 분석 방법론 | |
| 시각화 | 교차표, mosaic, stacked bar plot |
| 수치화 | 카이제곱검정 |
범주 feature로 범주 target과의 상관관계를 안다는 것.
사실 직관적으로 그래프가 떠오르지는 않는다.
그래프의 y label은 '어느정도의 양인가'를 나타내는 게 일반적이고,
그래서 범주로 범주를 예측한다는 것은 상당히 이질적이다.
하지만 세상은 그렇게 친절하지 않지.
우리는 결혼을 하고 안하고가 이직 결정에 영향을 미치는지,
성별에 따라 속하는 집단이 달라지는지가 알고 싶을 수밖에 없다.
따라서 범주와 범주의 관계를 증명하는 신박한 도구들이 있다.
- 시각화
1. 교차표(crosstab)
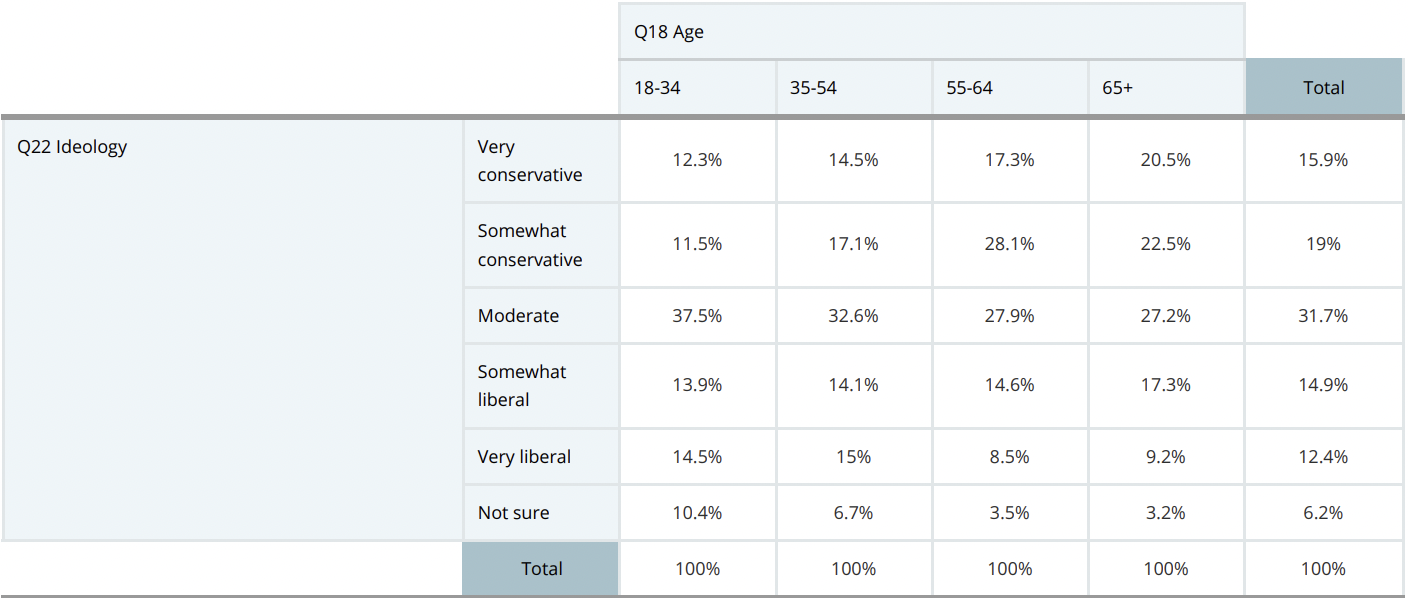
사실 교차표는 시각화 도구는 아니다. 그보단 집계 방식에 가깝지.
어렵게 설명할 것도 없다. 우리가 흔히 '표'하면 떠올리는 그 모양이 바로 교차표다.
x의 요소와 y의 요소가 겹치는 지점에 값을 쓴 것 말이다.
하지만 범주 → 범주 가설에서는 시각화든 수치화든 교차표로부터 시작해야만 한다.
# 두 범주별 빈도수를 교차표로 만든다.
pd.crosstab(df[target], df[feature])
# normalize= 파라미터를 통해 빈도수가 아닌 비율을 나타낼 수 있다.
pd.crosstab(df[target], df[feature], normalize=columns) # 열끼리 더하면 1
pd.crosstab(df[target], df[feature], normalize=index) # 행끼리 더하면 1
근데 찾아보다 보면 normalize 옵션은 그냥 True 주는 경우도 많은 듯?

2. 모자이크플롯(mosaic)
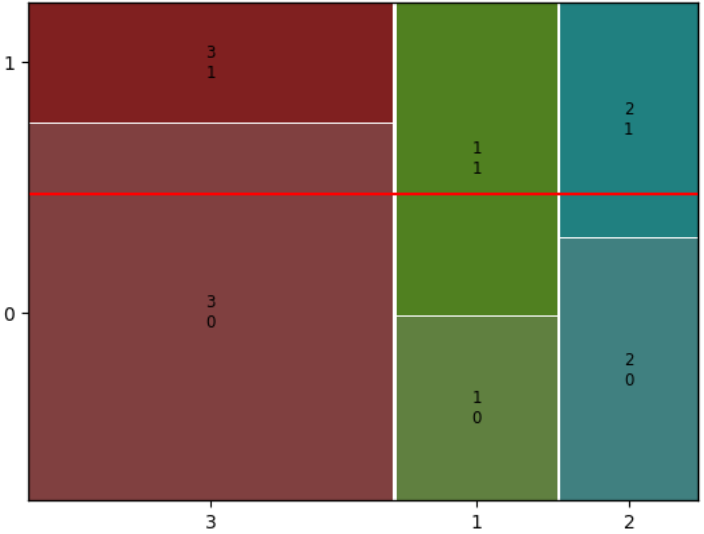
이 교차표를 기반으로 시각화한 것이 mosaic plot이다.
읽는 법이 다소 독특한데, x축이 feature의 범주들이 차지하는 비율,
y축이 그 feature의 범주들이 y에 대해 어떤 비율을 가지는지이다.
다시말해 위 표는 x=3인 그룹은 평균보다 많이 y=0에 속해 있고,
다른 두 그룹은 y=1인 비율이 높다.
from statsmodels.graphics.mosaicplot import mosaic
mosaic(df, [feature, target])
plt.axhline(1- df[target].mean())
plt.show()
mosaic는 plt나 sns가 아니라,
statsmodels.graphics.mosaicplot에 속해 있다. 따로 import해 줘야 하는 점을 주의하자.
그래서인지 문법도 특이하게 [x, y]의 리스트를 받는다.
※ axhline 사용 시 주의할 점.
plt.axhline()의 인자가 매번 똑같이 들어가지는 않는데,
특히 y가 1과 0으로 된 데이터일 경우에 조심해야 한다.
1의 비율을 나타내려면, (df[target].mean())이 맞지만
0의 비율을 나타내려면 (1 - df[target].mean())을 주어야 함을 명심하자.
3. 100% Stacked bar
범주와 범주의 관계를 나타내는 흥미로운 방법이 하나 더 있는데,
누적형 바플롯을 그려서 항목이 전체 중 차지하는 비율을 보여주는 것이다.

만드는 방법은 pandas에서 자체적으로 가진 plt 기능을 쓰면 된다.
crosstab이 데이터프레임을 반환하므로.plot.bar()를 쓸 수 있고, 인자로 stacked = True를 주면 된다.
temp = pd.crosstab(df[feature], titanic[target], normalize = 'index') # x와 y위치 주의
temp.plot.bar(stacked=True)
plt.axhline(1-titanic['Survived'].mean(), color = 'r')
plt.show()
- 수치화
카이 제곱 검정(Chi2_contingency, Chi-squared test)
카이제곱 검정. 이름은 멋지지만 원리는 꽤 간단하다.
x와 y가 관계가 없을 때 관측되는 데이터를 기대빈도라고 한다.
카이제곱 통계량은 쉽게 말해 기대빈도에서 실제 빈도가 얼마나 차이나는지
(즉, x와 y가 얼마나 관계있는지)를 묻는 것이라 할 수 있다.
그러니 당연히

이렇게, 기대빈도 대비 관측빈도량을 알 수 있는 식을 가진다.
오늘도 마찬가지로 계산은 함수가 해 준다 ㅋㅋㅋ...
늘 수치화 검정에서 사용하던 spst을 이용하면 된다.
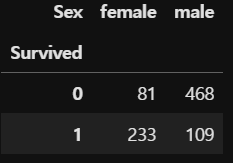
# 먼저 교차표 집계- 빈도를 세므로 normalize 하면 안 된다.
table = pd.crosstab(titanic['Survived'], titanic['Pclass'])
display(table) # 데이터프레임이므로 display()
# 카이제곱검정
spst.chi2_contingency(table)
코드에서 보이듯이, 교차표를 다른 변수로 선언하고는 그걸 냅다 집어넣으면 된다.
오오 원터치함수시여...

다른 수치화 가설 검정 도구가 그렇듯이 score과 p-value를 튜플 형태로 뱉는다.
다만 하나 더, '자유도'라는 것을 뱉는다.
이건 뭐... 어렵게 말하자면 다중공선성처럼 다른 범주에 의해 예측가능한 수를 뺀 범주 수고,
쉽게 말하자면 한 범주 내의 카테고리 수 -1한 값이다.
p-value가 가장 중요한 판단지표인 것은 지금까지 본 가설 검정 도구들과 동일하다.
카이제곱 점수는 얼마나 독립에서 머냐니까... 당연히 클수록 대립가설에 가까워진다.
이변량 분석 : 숫자 → 범주
| 숫자 → 범주 이변량 분석 방법론 | |
| 시각화 | kdeplot, histplot |
| 수치화 | - |
숫자 → 범주 가설일 때는 수치화 검정은 없다. 나이스
시각화로 kedplot과 histplot이 있는데... 속성이 비슷하므로 묶어서 보자.
def num2obj(feature): # kde plot 2종과 histplot 생성
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
plt.ylabel('Attrition')
sns.kdeplot(data=data, x=feature, hue='Attrition', common_norm=False)
plt.grid()
plt.subplot(1, 3, 2)
plt.ylabel('Attrition')
sns.kdeplot(data=data, x=feature, hue='Attrition', multiple='fill')
plt.axhline(data[target].mean(), color='r')
plt.grid()
plt.subplot(1, 3, 3)
sns.histplot(data=data, x=feature, bins=20, hue=target, multiple='fill')
plt.axhline(data[target].mean(), color='r')
plt.grid()
plt.tight_layout()
plt.show()
내가 만든 반쪽짜리 함수.
feature는 변수로 받게 해 놓고hue, 그러니까 target은 직접 입력하는 모습이 인상적이다.
코딩마스터스때도 그렇고 하드코딩하는 습관을 빨리 뜯어고쳐야 한다. 무근본 독학으로 시작해서 그렇다.
여튼 위 함수 인자로 'DistanceFromHome', 그러니까 통근거리를 주고 이직율과의 차이를 보았다.
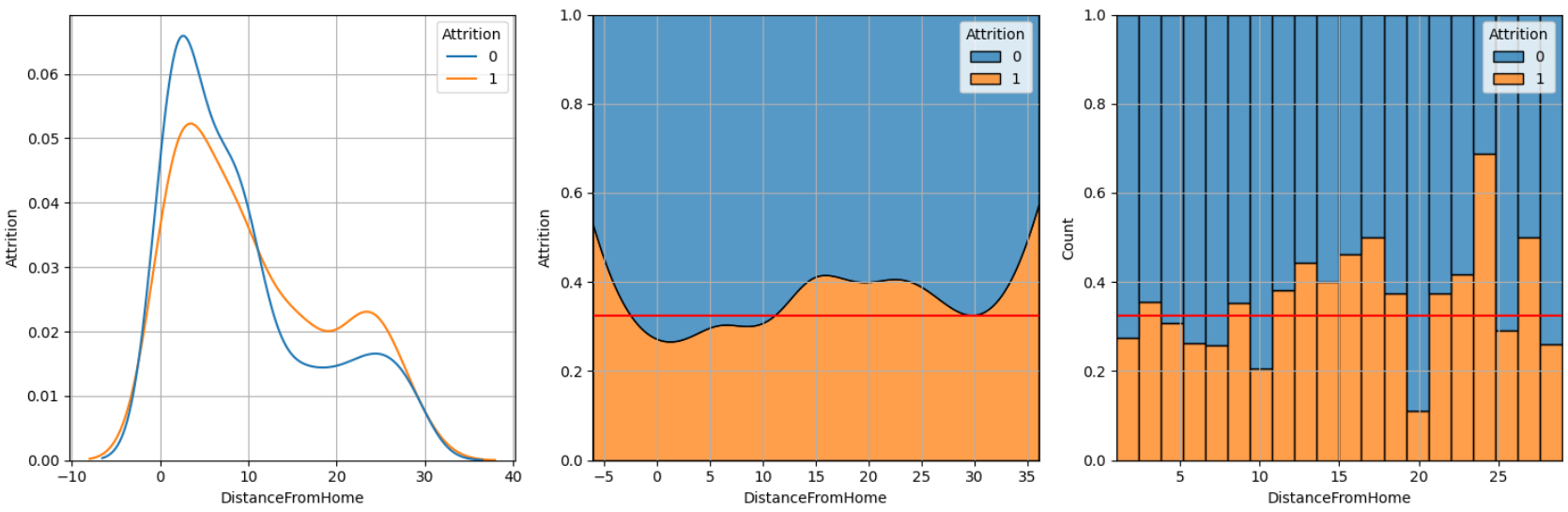
열심히 읽어 보자.
첫 그래프, kde인데 multiple 파라미터 없이 common_norm=False 옵션을 주었다.
두번째는 같은 kde지만 multiple='fill'을 지정한 경우
세번째는 두번째와 같은 인자에서 kde만 histplot으로 바꾸고 bins를 설정해준 것.
같은 자료이니만큼 15~25마일 구간에서 이직율이 높은 것을 알 수 있다.
다만 histplot에서만 보이는 구간이 있는데, 딱 20마일인 지점에서는 이직율이 낮다.
무슨 이유일까? 저기부턴 오히려 통근하기 편해지는 교통수단이 있나?
아니면 저 지점부터 교통비를 지원해 주나? 하지만 그러면 그 다음에 급등하는 것이 설명이 안 된다.
강사님께서는 이럴 때 담당자를 찾아가 도메인 지식을 공유하라고 하셨지.
솔직히 그건 좀 재밌겠다.