
목차
1. 데이터 분석 개요
2. 일변량 데이터 분석 : 수치형
3. 일변량 데이터 분석 : 범주형
4. 가설 검정
새로운 강사님이 오시는 첫 날을 휴가로 보내고,
홀로 초면인 한기영 강사님을 뵌 나.
이전 이장래 강사님과는 약간 다른 스타일이신데, 원리에 굉장히 많은 시간을 할애하신다.
뚝딱뚝딱 코드 치는 거에도 익숙해졌다 싶었는데,
또 이런 강의를 들으니 낯설기도 어렵기도 하다.
내가 뭘 할 수 있니열심히 요약해야지, 어제 안 한 부분까지 해서 싹 훑어보자.
데이터분석 개요
데이터분석, DX 컨설턴트의 주 업무 중 하나이자, 지금까지 달려 온 이유.
데이터의 종류(수치형/범주형)에 따른 적절한 분석 방법을 익혀
비즈니스에 도움이 되는 인사이트를 도출하는 것이 목적이다.
- CRISP-DM
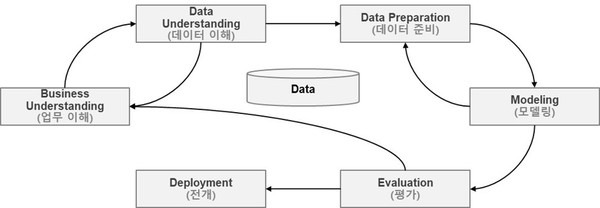
CRISP-DM크리스프디엠은 Cross Industry Standard Process for Data Mining이란 뜻으로,
말 그대로 데이터 분석 전반에서 쓰이는 표준 프로세스이다.
단계는 전반적으로 다음과 같은데,
1. 업무 이해
비즈니스 문제점을 정의하고 데이터분석 방향성과 목표를 결정,
가설(x → y)을 수립하여 데이터 분석을 정의하는 단계
2. 데이터 이해
데이터의 원본 식별 및 취득, 이에 대해 EDA와 CDA를 수행한다.
* EDA : 탐색적 데이터 분석 - 데이터 분포, 결측치, 이상치 파악, 가설 확인
* CDA : 검증적 데이터 분석 - EDA에서 처리하지 못한 과정 처리, 가설 검정
3. 데이터 전처리
모델 학습을 위해 결측치 처리, 가변수화, 스케일링, 데이터 분할 등을 수행한다.
* 결측치 처리 : dropna(), fillna(), ffill(), bfill()
* 가변수화 : pd.get_dummies(), le = LabelEncoder(), le.fit_transform()
* 스케일링 : minmaxscaler(), standardscaler() 생각해 보니 어제 이걸 빼먹었네
* 데이터 분할 : train_test_split()
수행 후 반드시
결측치가 없고, 모든 값이 숫자이며, 값의 범위가 최대한 일치해야 한다.
4. 모델링
학습용으로 다듬은 데이터를 모델에게 학습시켜 데이터의 패턴을 찾는다.
오차를 최소화하기 위한 조정을 가한다.
결과물로 모델(알고리즘)이 수학식으로 표현된다.
* 지도학습 , 비지도학습의 구체적인 모델은 추후에 다루기로 하자.
5. 모델 성능 평가
미리 나누어 둔 test set을 통해 모델의 성능을 평가한다.
모델을 비즈니스에 적용했을 시의 기대 가치를 평가한다.
6. 배포 및 관리(Deployment)
프로젝트 결과물을 최종 확정하고, 환경적 파이프라인, 모델과 배포의 목표 충족 여부를 확인한다.
모니터링 계획 수립, 품질 관리 기준 결정 등을 수행한다.
단변량 데이터분석 : 수치형
수치형 데이터를 단변량 분석할 때는 두 가지 방법이 있다.
1. 정보의 대푯값(기초통계량) 활용 : 평균, 중앙값, 최빈값, 사분위수 등 - boxplot으로 시각화
plt.boxplot(temp['Age'] , vert = False) # 횡으로 나오게 하는 옵션
plt.grid()
plt.show()

boxplot은 박스가 4분위수를 나타내고, 양쪽의 '수염'이 정상치의 범위를 나타낸다.
2. 도수분포표 활용 : 구간별 빈도수 확인 - histogram과 kdeplot으로 확인
plt.figure(figsize = (8,8))
plt.subplot(2,1,1)
sns.histplot(boston[var], bins = 30, kde = True)
plt.grid()
plt.subplot(2,1,2)
sns.boxplot(x = boston[var])
plt.grid()
plt.show()
히스토그램과 KDE plot(Density plot)은 변수의 분포를 보여준다.
히스토그램은 특히 애용되지만, bins 파라미터 설정에 따라 완전히 다른 결과가 나오니 주의.
단변량 데이터분석 : 범주형
범주형 데이터의 소양은 단 하나다.
그것은 바로 빈도.
따라서 .value_counts()가 수치형의 .describe()같은 역할을 한다.
여기서 나가는 꿀팁.
value_counts()에 normalize=True 파라미터를 주면 범주들의 비율도 볼 수 있다.
titanic['Pclass'].value_counts()
titanic['Pclass'].value_counts(normalize = True)

이 경우 시각화는 barplot으로 한다.
특히 복잡한거 건너뛰고 냅다 데이터 집어 넣으면 바플롯 뽑아주는 sns.countplot(). 소중하다.
sns.countplot(x='Pclass', data=titanic)
plt.grid()
plt.show()

가설 검정
그 옛날 논리학 지문에서 본 적 있는 가설 검정.
이변량 분석에 쓰이는 것이지만, 오늘 하기도 했고 이변량은 할게 많으니 오늘 한다.
사전학습 때 이 부분에서 엄청 헤맸었다. 국어쌤 체면이 말이 아니다.
드가자.
- 가설
데이터분석적 의미에서, 가설이란 'feature x가 target y와 관련이 있을 것이다.'로 귀결된다.
따라서 가설 검정이란 x와 y의 관계성 여부를 확정하고, 그 정도를 가늠하는 과정이라 할 수 있다.
자 그럼 가설 검정 과정에 들어가기 전에, 용어 하나만 보고 가자.
귀무가설 = H0 = 영가설 = 기존 가설
x가 y와 무관할 것이라는 가설. 가설 검정이 되지 않은 feature는 당연히 귀무가설이 채택된 상태.
대립가설 = H1 = 연구가설 = 새로운 가설
x가 y와 유관할 것이라는 가설. 가설 검정 결과 실제로 유관하다면, 귀무가설을 버리고 대립가설을 채택.
- 가설 검정
'엄마 나 100점 받았어. 토익에서.' 하상욱의 시같다.
이 사례에서 보이듯, 모든 수치는 수치 자체보다는...
남들은 보통 어느정도 되는지(분포)와 얼마부터 높은거고 얼마부터 낮은지(기준)이 중요하다.
그럼 생각해보자.
대립가설을 주장하려면, 즉 x가 y와 유관하다고 말하려면?
x에 따라 y값이 차이나면 된다.
그 '차이라는 수치'가 유의미하다고 말하려면?
분포와 기준이 필요하다.
따라서 가설 검정 과정은 x가 y에 미치는 영향력의 분포와 기준을 보는 것이다.
이때 p-value라는 것이 쓰인다.
쉽게 말하자면, 분포 기준으로 봤을 때 귀무가설에서 얼마나 예외적인 상황인지를 보여주는 지표이다.
더 쉽게 말하자면 귀무가설이 맞다는 전제 하에 실제 관측 데이터가 나타날 확률을 나타낸다. 하나도 안 쉽다.
아직 좀 애매하니, 예를 들어 보자.
우리의 친구 철수는 토익 650~700을 전전하고 있다..
그런데 여기서 웬걸, 무당 민규가 갑자기 '비가 오면 철수 성적이 오른다.'라고 주장하기 시작했다.
(대립 가설, '비 내림(x)은 민규의 토익 성적(y)에 영향을 준다.')
데이터 분석가인 우리는 뭘 할까?
뭐하긴 뭐 해. 비 올 때 철수 성적이랑 비 안 올 때 철수 성적 기록해야지.
그렇게 놀랍게도 300번의 토익 시험을 친 철수
이때 우리는 철수의 성적이 650~700 사이에서 일정하게 유지되는 것(성적의 분포)을 바탕으로 생각한다.
어느 비 오는 날 철수가 토익에서 750점을 맞았다고 하자.
민규가 당당하게 말한다, "봐라, 내가 말했지? 비가 오면 철수 성적이 오른다고!"
하지만 여기서 중요한 건, 우리가 모은 여러 날의 성적 데이터가 정말로 그런 경향을 보이는지 확인하는 것이다. 즉, 철수가 750점을 받은 날이 단순한 우연인지, 아니면 정말로 비가 성적에 영향을 미쳤는지 판단해야 한다.
이때 p-value를 통해 이 상황을 판단한다.
"비가 성적에 아무 영향이 없다고 가정할 때, 철수가 우연히 750점을 맞을 확률은 얼마나 될까?"
즉, 귀무 가설이 맞다는 전제 하에서 "이 정도로 높은 성적"이 나타날 가능성이 얼마인지를 계산하는 것이다.
솔직히 650에서 700이던 철수가 750 맞을 확률은 아주 작진 않은 듯하다.
'역시 비는 상관없었어.'(귀무가설 채택)
근데 만약 그가 900을 맞았다면?
아까보다 p-value가 더 낮다. 그래도 한 번 정도는뽀록운으로 맞을 수도 있...을까?
근데 900이 여러번이었다면? 다 비 오는 날이었다면?
p-value가 아주 낮다.
'이제는 민규의 가설을 인정할 수밖에 없겠군.'(대립가설 채택)
대충 쓰려고 했는데 엄청 길어졌다.
뭐 대충 이런 원리란거지~
그렇다면 내일은, 이변량 데이터 분석이다.
방금 한 이야기는 이변량 데이터 분석에서도 첫 단계라 할 수 있는 상관분석 단계에서 일어날 일의 일각이다.
내일을 기대하시라 흑흑