
ADsP 시험도 점점 다가오는 해피(?) 할로윈.
힘내서 가보자.
히든 레이어 심화
지난 시간에, 우리는 law data의 모든 feature가 히든 레이어에 할당되는 것을 보았다.
이를 Fully Connected라고 하며, Dense를 활용하여 모델을 구성한다.
하지만 히든 레이어마다 서로 다른 feature를 할당할 수도 있다.
이를테면, '집값에 영향을 주는 요인'을
1. 방 수, 면적, 인테리어
2. 지하철 접근성, 주변 편의시설, 공원 접근성
으로 나눌 수 있다.
이를 Locally Connected라고 한다.

이것은 히든 레이어가,
나름대로 law feature들을 조합하여 의미있는 새로운 feature를 만들어 낸 것이라고 볼 수 있다.
이런 측면에서 보았을 때,
딥러닝에서는 히든 레이어를 생성하는 과정에서 feature engineering이 진행된다.

딥러닝 이진 분류
다 아는 이야기를 해 보자.
함수란 입력 x를 넣었을 때 출력 y를 뱉어내는 것이다.
학생 시절 상자 함(函)자를 통해서 배웠었지.
다시말해, 함수의 역할이란 x를 y로 변환(transformation)하는 것이다.
딥러닝의 식은 가중치를 스스로 조절하기에,
그 결과가 아주 작거나 클 수 있다.
하지만 우리가 원하는 산출값은 정해져 있지.
이를테면 이진 분류라면 0이나 1로 나와야 한다.
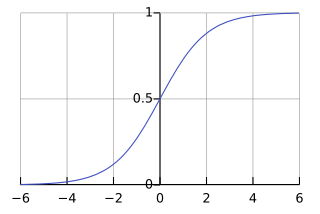
이때 데이터를 시그모이드 함수에 통과시키면
x의 범위는 ±inf 이고 y의 범위는 0 ~ 1인 데이터로 변환된다.
이게 아웃풋 레이어의 활성함수가 하는 역할이다.
(지난 시간에 봤듯, 히든 레이어에서는 선형 함수를 비선형으로 바꾸어 주는 역할을 한다.)
아웃풋 레이어의 활성함수는 다음과 같다.
이진 분류 : sigmoid
다중 분류 : softmax
회귀에서는 함수를 일반적으로 쓰지 않으나,
결과가 양수로만 나와야 하면 relu 사용
한편, 손실 함수는 오차를 계산하는 방식으로
컴파일 과정에서 설정했다.
이진 분류 모델에서의 오차는 값이 아니라 '몇 개가 틀렸다.'의 영역이다.
그러니 손실 함수도 다를 수밖에.
이진 분류 모델의 손실 함수는 binary_crossentropy를 사용한다.
# 모델링
nfeatures = x_train.shape[1]
model = Sequential( [Input(shape = (nfeatures,)),Dense( 1, activation= 'sigmoid')])
# 모델 컴파일
model.compile(optimizer = Adam(learning_rate=0.01), loss = 'binary_crossentropy')
# 모델 학습
history = model.fit(x_train, y_train, epochs = 50, validation_split=0.2).history
출력 함수가 sigmoid라는 것은, 0과 1 사이의 확률값이 출력된다는 뜻이다.
성능 평가를 위해서는 그 확률값을 이진값으로 변환해 줄 필요가 있다.
이건 수동으로 가능하다.
# 예측 및 검정
pred = model.predict(x_val)
pred = np.where(pred >= .5, 1, 0) # 확률값을 0 or 1로 변환
print(classification_report(y_val, pred))
이때 0,5가 아닌 다른 값으로 나눌 수도 있겠지? recall을 높여야 한다거나...
이또한 분석가에게 달린 일이라고 할 수 있겠다.
정리하자면, 이진 분류 코드와 회귀 코드의 차이는 세 가지이다.
1. 모델링 시 Output layer에 activation = 'sigmoid' 사용
2. 컴파일 시 loss = 'binary_crossentropy' 사용
3. 평가 전 pred = np.where(pred >= .5, 1, 0) 으로 확률값을 분류
이를 바탕으로, 이진 분류 모델 생성 과정을 한 블록에 넣어 보자.
# 모델 구조 생성
model1 = Sequential([
Input(shape=(n,)),
Dense(5, activation='relu'),
Dense(1, activation='sigmoid')
])
# 모델 컴파일
model1.compile(optimizer=Adam(learning_rate=0.001), loss='binary_crossentropy')
# 학습 및 시각화
history = model1.fit(x_train, y_train, epochs=50, validation_split=.2, verbose=0).history
plt.plot(history['loss'], label='Train_err', marker='.')
plt.plot(history['val_loss'], label='Validation_err', marker='.')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
# 성능확인
pred = model1.predict(x_val)
pred = np.where(pred >= 0.5, 1, 0)
print(classification_report(y_val, pred))
딥러닝 다중 분류
다중분류의 가장 큰 특징이라면,
Output layer의 노드 수가 1이 아니라, 범주 수만큼이라는 것이다.
참 당연한 사실인데, 자주 까먹는단 말이지.


코드 측면에서 보면, 이진 분류와 다섯 가지가 다르다.
1. 모델링 시 Output layer에 activation = 'softmax' 사용
2. 모델링 시 Output layer의 노드 수는 클래스의 수만큼.
3. y에 대한 가변수화가 필요(라벨인코딩 / 원핫인코딩)
- 사실 이진 분류였어도 y가 문자였으면 0과 1로 바꿨어야 한다. 당연.
4. y 가변수화의 방법에 따라 컴파일 시 loss function이 다름
- 라벨인코딩 : sparse_categorical_crossentropy
- 원핫인코딩 : categorical_crossentropy(이 두 함수는 수학적으로 동일하다.)
# 메모리 정리
clear_session()
# Sequential
model = Sequential( [Input(shape = (nfeatures,)),
Dense( 3, activation = 'softmax')] )
# 모델 컴파일
model.compile(optimizer=Adam(learning_rate=0.1), loss= 'sparse_categorical_crossentropy')
# 모델 학습
history = model.fit(x_train, y_train, epochs = 50, validation_split=0.2).history
# 예측
pred = model.predict(x_val)
pred[:5]
시그모이드가 그랬듯, 소프트맥스도 다음과 같이 확률값을 반환한다.

이런 식으로.
한 행의 값들을 다 합하면 1이 되는 확률값이다.
따라서 우리는 이들을 0, 1, 2 등을 할당해 줘야 하는데,
이때 np.argmax()를 사용한다.
np.argmax()
특정 행/열에서 가장 높은 값의 인덱스를 반환한다.
따라서 axis 옵션을 1로 주면 한 행에 속한 각 열 중 가장 큰 값의 열 번호를 반환한다.
그래서 위 softmax 반환값에 다음을 실행해 준다.
pred = pred.argmax(axis=1)
pred
이를 반영한 코드블럭을 작성하면...
# 모델 구조 선언
model2 = Sequential([
Input(shape = (nfeatures,)),
Dense(8, activation = 'relu'),
Dense(8, activation = 'relu'),
Dense(3, activation = 'softmax')
])
# 모델 컴파일
model2.compile(optimizer=Adam(learning_rate=0.01), loss= 'sparse_categorical_crossentropy')
# 모델 학습
history = model2.fit(x_train, y_train, epochs = 90, validation_split=0.2, verbose=0).history
# 모델 시각화
plt.plot(history['loss'], label='train_err', marker = '.')
plt.plot(history['val_loss'], label='val_err', marker = '.')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend()
plt.grid()
plt.show()
# 예측 및 평가
pred = model2.predict(x_val)
pred = pred.argmax(axis=1)
print(confusion_matrix(y_val, pred))
print(classification_report(y_val, pred))