
클러스터링 실습
실습용 데이터를 바탕으로 비지도학습을 진행해 본다.
실습용 데이터 생김새

1단계
# 클러스터링에 사용할 데이터만 분리
x = data.loc[:, ['Age', 'Income', 'Score']]
# 클러스터링은 거리 기반이므로 스케일링
scaler = MinMaxScaler()
x_s = scaler.fit_transform(x)
# 모델 생성, 클러스터 수(k) 판별을 위해 평가지표 저장
kvalue = range(2, 21)
inertia, sil_score = [], []
for k in kvalue:
model = KMeans(n_clusters=k, n_init='auto')
model.fit(x_s)
pred = model.predict(x_s)
inertia.append(model.inertia_)
sil_score.append(silhouette_score(x_s, pred))
# 저장한 평가지표 시각화
plt.figure(figsize=(14, 5))
plt.subplot(1, 2, 1)
plt.plot(kvalue, inertia, marker='o')
plt.xlabel('K-value')
plt.ylabel('Inertia')
plt.subplot(1, 2, 2)
plt.plot(kvalue, sil_score, marker='o')
plt.xlabel('K-value')
plt.ylabel('Silhouette')
plt.grid(lw=0.3)
plt.tight_layout()
plt.show()
우선 전처리 단계 + 적절한 클러스터의 수(k) 찾기를 수행한다.
모델 생성 부분만 조금 보자.
kvalues에 가능한 클러스터 개수 범위 지정(주관적)
평가지표를 저장할 리스트 두 개 생성
kvalues를 순회하며 fit과 predict → 클러스터 개수별 평가지표를 저장
기계적으로 할 수 있어야 한다.
이 과정을 통해 아래와 같은 그래프를 얻고, 이를 바탕으로 k를 정한다.

2단계
# k = 6으로 결정
k=6
# 예측
model = KMeans(n_clusters=k, n_init='auto')
pred = model.fit_predict(x_s)
# 예측 결과를 데이터프레임으로 만들고
pred_df = pd.DataFrame(pred, columns=['Cluster'])
# 원본 데이터와 합치기
x_clusterd = pd.concat([x, pred_df], axis=1)
# 예측 결과는 카테고리 타입으로 변경
x_clusterd['Cluster'] = pd.Categorical(x_clusterd['Cluster'])
k를 6으로 정했으니, 진짜 KMeans로 클러스터를 나눈다.
그 결과값을 기존 데이터프레임에 concat함으로써 클러스터 열이 생긴다.

이제 클러스터 별 변수들의 특징을 한번 살펴보자.
plt.figure(figsize=(10,4))
plt.subplot(1, 2, 1)
sns.kdeplot(x= feature, data = x_clusterd, hue='Cluster')
plt.grid()
plt.subplot(1,2,2)
sns.boxplot( x= feature, data = x_clusterd, hue = 'Cluster')
plt.grid()
plt.tight_layout()
plt.show()
그래프는 kde와 box를 사용한다.
feature = 'Age'
| 클러스터 | 특징 |
| 0 | 연령대가 고르게 분포되어 있음 |
| 1 | 30대 위주 |
| 2 | 40대 ~70대 위주 |
| 3 | 20대 |
| 4 | 연령대가 고르게 분포되어 있음 |
| 5 | 20대. 3번 클러스터보다 많음 |
feature = 'Income'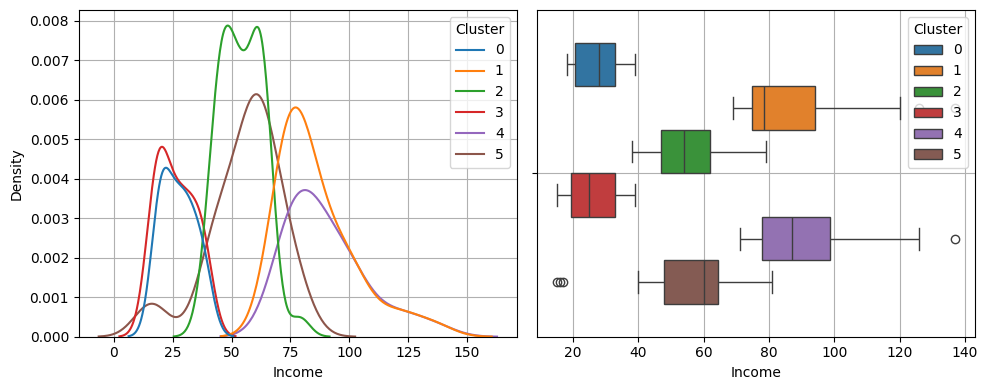
| 클러스터 | 특징 |
| 0 | 저소득구간 |
| 1 | 고소득구간 |
| 2 | 중간소득구간 |
| 3 | 저소득구간 |
| 4 | 고소득구간 |
| 5 | 중간소득구간 |
feature = 'Score'
| 클러스터 | 특징 |
| 0 | 저득점 |
| 1 | 고득점 |
| 2 | 중간 |
| 3 | 고득점 |
| 4 | 저득점 |
| 5 | 중간 |
mosaic(x_clusterd, ['Cluster', 'Gender'])
plt.show()
| 클러스터 | 특징 |
| 0 | 평균 |
| 1 | 상대적으로 남자가 많다 |
| 2 | 평균 |
| 3 | 상대적으로 여자가 많다 |
| 4 | 상대적으로 남자가 많다 |
| 5 | 평균 |
이상의 사항들을 정리해 보자.
| 클러스터 | 나이 | 소득 | 구매점수 | 성별 |
| 0 | - | 저소득 | 낮음 | - |
| 1 | 30대 | 고소득 | 높음 | 남 위주 |
| 2 | 40대 이상 | 중간소득 | 중간 | - |
| 3 | 20대 | 저소득 | 높음 | 여 위주 |
| 4 | - | 고소득 | 낮음 | 남 위주 |
| 5 | 20대 | 중간소득 | 중간 | - |
이렇게 클러스터별로 변수의 분포를 살펴보니,
집단마다 유의미한 태그를 붙일 수 있었다.
<마케팅 전략 수립>
위처럼 집단이 나뉘고 나면 적절한 마케팅 전략을 세울 수 있을 것이다.
이를테면
0번 : 저소득에 구매도 적은 집단이다.
가격에 민감하지만, 가성비가 뛰어난 제품이나 서비스에는 충성도가 높은 경향을 보이는 집단이다.
가격 민감성을 반영한 할인 및 묶음 상품 프로모션으로 더 높은 가치를 제공할 수 있을 것이다.
또한 타사 제품과의 가격 비교 마케팅이 유효할 것으로 보인다.
제품의 카테고리는 생필품을 중심으로 두되, 분할 결제 및 저가 구독 서비스를 통해 구매 허들을 낮추어야 한다.
샘플이나 체험 상품을 제공하는 것 또한 유효하며,
거시적으로는 이런 계층만을 대상으로 하는 세컨드 브랜드를 활용할 수도 있을 것이다.
1번 : 구매력도 소비지수도 높은 30대 남성 위주 집단이다.
최신 기술과 취미활동에 관심이 많고, 신뢰할 수 있는 브랜드에 대한 충성도가 높은 집단이다.
따라서 중고가 전자기기나 취미용품 위주의 마케팅을 펼치는 것이 적절하고,
높은 수준의 고객서비스를 제공한다면 다른 집단에 비해 더 큰 충성도를 확보할 수 있을 것이다.
또한 결제 과정에서 많은 이탈을 보이는 집단이기에 손쉽고 빠른 결제를 반드시 제공할 수 있어야 한다.
금융 서비스나 자산 관리 프로그램 등 그들의 성취를 더욱 높이는 데 도움을 주는 서비스가 유효할 수 있다.
2번 : 고연령 중위소득 집단이다.
실용성과 가성비를 중시하며, 가정과 자산 관리에 대한 관심이 높다.
따라서 가성비 마케팅을 중심으로 하되 특히 제품의 내구성과 긴 품질 보증 기간을 내세운 것이 유효하다.
가족 마케팅이 가능한 집단이며 가사의 편리함을 증진시키는 제품,
건강과 웰빙을 메인으로 하는 제품이 적절할 수 있다.
한편 오프라인 쇼핑과 온라인 쇼핑에 둘 다 발을 걸친 집단이므로 양자의 균형을 맞출 필요가 있다.
3번 : 20대 저소득 구간이지만 구매가 많은 여성 위주 집단이다.
경제적 부담을 최소화하면서도 감성적이고 트랜디한 요소가 중요하게 작용하는 집단이다.
패션 및 뷰티 분야에서 가성비 높은 제품이나 1+1 프로모션 등이 좋은 효과를 보일 수 있다.
또한 모바일과 SNS 중심의 소비패턴을 보이기 때문에 인플루언서 협업과 SNS 마케팅이 유효하다.
4번 : 다양한 연령의 고소득 집단이자, 구매율이 낮은 남성 위주 집단이다.
경험과 가치 중심의 소비를 보이는 집단이므로 프리미엄 전략이 유효하다.
연령대가 다양하므로, 개인화된 맞춤형 솔루션을 제공하는 것이 중요하다.
개인의 필요에 맞춘 특별 서비스나 VIP 혜택을 강조하여 구매 전환을 유도할 수 있을 것이다.
긴급성(한정된 시간 할인)이나 희소성(한정판 제품) 전략으로 구매를 촉진할 수 있다.
한편 자산 증가에 관심이 많은 집단이기도 하므로 고가 제품을 장기적인 투자로 포지셔닝하는 마케팅이 좋다.
5번 : 개인적으로 마케팅이 가장 어렵다고 생각한다. 20대라는 특징 외에는 별다른 특이점이 보이지 않는다.
20대라는 점에서, 트렌드 중심, SNS 중심 전략 정도가 유효할 수 있겠다.
이런 요소를 pairplot으로 시각화할 수도 있다.

DBSCAN

DBSCAN(Density-based spatial clustering of applications with noise)은 밀도 기반 알고리즘으로,
epsilon 범위의 원을 기반으로 원 안에 minPoints 만큼의 데이터가 존재하는지를 확인한 후,
존재한다면 각 포인트를 중심으로 epsilon 범위의 원을 그려 이 과정을 반복하는 방식이다.
minPoints를 만족하지 않는다는 것은
최소한의 밀도를 만족하지 못하는(= 군집이라고 볼 수 없는) 자료이므로 noise로 처리한다.
거리 기반이라서 덩어리 형태 데이터만 처리할 수 있는 K-Means와 다르게,
비정형 데이터를 효과적으로 처리할 수 있다.
주의해야 할 DBSCAN의 파라미터로는 eps(epsilon)가 있다.
DBSCAN이 돌아가는 원의 크기를 정하는 것으로,
원의 크기가 작으면 노이즈로 판정되는 것들이 많아지고
원의 크기가 크면 구분이 제대로 안될 수 있다.
def dbscan_plot(x, y, eps) :
model = DBSCAN(eps=eps, min_samples=3)
model.fit(x)
clusters = model.labels_
plt.figure(figsize = (8,6))
plt.scatter(x['x1'], x['x2'], c=clusters, alpha=0.5)
plt.grid()
plt.show()
dbscan_plot(x, y, eps = 0.1)
이때 eps 값에 따라 분류가 어떻게 달라지는지 보자.
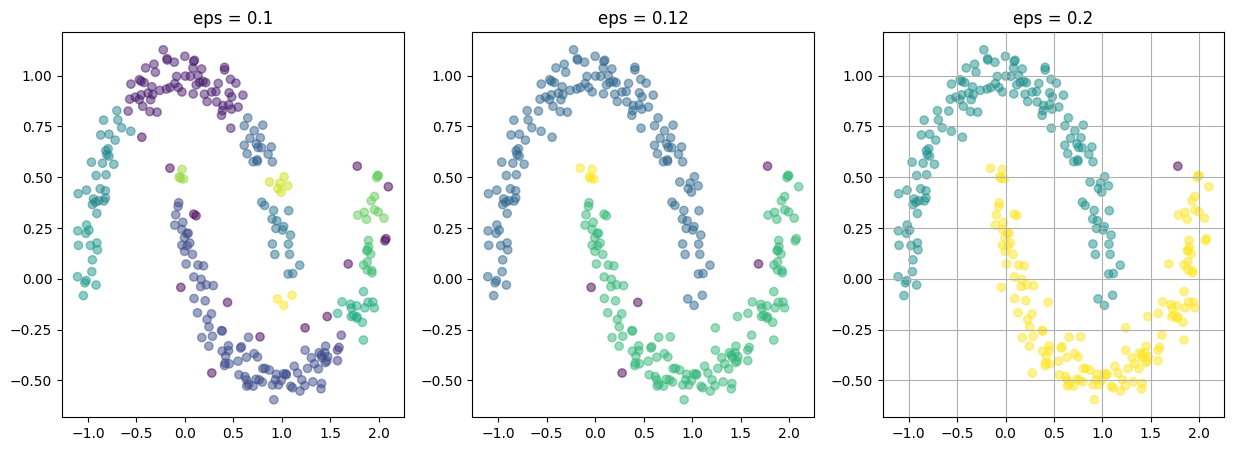
eps가 높다는 것은 허용하는 거리가 높다는 셈인데,
그래서 값을 적절하게 높임으로써 비정형 데이터를 클러스터링할 수 있었다.
이상탐색
이상탐색은 말 그대로 데이터를 정상/비정상으로 평가하는 것이다.
이 문제의 유형은, 분류형 지도학습 문제처럼 보인다. 그것도 손쉬운 이진 분류.
하지만 이상탐색에는 비지도학습의 측면을 가지고 있는데,
학습 방법이 비지도학습에 가깝기 때문이다.
이상 탐색의 '이상'은 '비정상'이기에, 언제나 데이터의 양이 극도로 부족하다.
다시말해 지도학습의 방법으로 간단히 비정상 나누기는 힘들단거지.
그렇기에 우리는 정상 데이터만으로 정상 데이터의 범위를 설정(비지도학습)하고,
거기서 벗어나면 비정상임을 탐지하는 방식으로 접근해야 한다.
이상탐지에서 중대한 장애물로 작용하는 것이 몇가지 있다.
첫째, 제대로 된 Label이 있어야 한다.
보통 비정상 데이터라는 것은 자동으로 수집되지 않고 수동을 관리되는 경우가 많다.
비지도학습으로 이상 탐지 모델을 만들 수야 있겠지만,
그 모델을 평가하려면 Label이 정답 역할을 해 줘야 한다.
그런데 전술했듯 수동으로 관리된 데이터란 여러 측면에서 제대로 된 label로 보기 힘들다.
둘째, 성능을 높이기 어렵다.
방금 본 label 문제로 성능 평가 자체가 어렵다.
또한 '이상'을 탐지하는 모델 특성상 accuracy가 아닌 recall을 평가지표로 써야 하는데,
이 지표는 형편없이 낮은 경우가 많다.
이상탐지 알고리즘
이상탐지의 제1단계는, Abnormal이 어느정도인지 평가하는 것이다.
만약 Abnormal이 극단적으로 부족한 게 아니라면,
이상탐지까지 갈 필요 없이 리샘플링 등을 통해 지도학습으로 분류 모델을 만들면 된다.
하지만 Abnormal이 극도로 부족할 때, ML과 DL의 다양한 알고리즘을 활용해야 한다.
그중에 대표적인 ML 알고리즘인 Isolation Forest를 알아보자.
Isolation Forest의 이상탐지 과정은 다음과 같다.
1. Train Set에서 데이터 샘플링
약 256개 정도가 충분한 샘플이라고 알려져 있다.
2. Isolation Tree 생성
Decision Tree처럼 feature를 바탕으로 split을 진행하는 것은 같다.
그런데 Isolation Tree는, 불순도를 기준으로 삼지 않고 랜덤하게 데이터를 쪼갠다.
데이터가 하나만 남아 완전히 고립될때까지.
비슷한 특성을 가지고 있는 데이터가 많다면, 고립될 때까지 더 많이 쪼개야겠지.
하지만 Abnormal한 값이라면, 훨씬 적게 쪼개는 것으로도 고립을 만들 수 있다.
다시말해, Abnormal은 Isolation Tree의 깊이가 얕은 데이터인 것이다.
이렇게 트리를 여러 개 만들어 IsolationForest를 형성하여
평균 depth를 구해 기준으로 사용한다.
3. Score를 기반으로 Abnormal 구분
경로의 길이를 max 1인 점수로 만들어,
점수가 1에 가까울수록 이상치라고 판단한다.
# 모델링
model = IsolationForest(contamination = 0.1, n_estimators = 50 )
model.fit(X1)
pred = model.predict(X1)
pred
contamination은 설정할 abnormal 데이터의 비율이고, n_estimators는 트리의 수이다.

-1이 abnormal인데, 실전에서는 정상을 0, 비정상을 1로 두는 경우가 많으므로 변환시켜준다.
pred = np.where(pred == 1, 0, 1)
# 모델 시각화
model_visualize(model, X1['v1'], X1['v2'], 'Isolation Forest')
각각의 영향력을 보기 위해 몇 번의 시도를 해 보면
| contamination=0.1 // n_estimators=100 | contamination=0.3 // n_estimators=100 |
 |
 |
| contamination=0.1 // n_estimators=5 | contamination=0.01 // n_estimators=100 |
 |
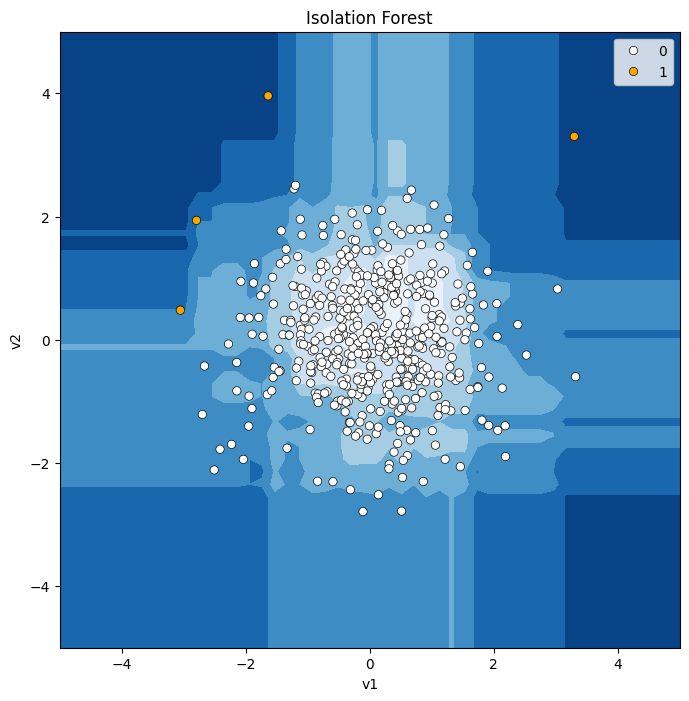 |
contamination은 직관적이다. 이상치를 몇 %로 설정할 것인지를 나타내는 것이니까.
n_estimators가 낮으면, 정상 범위가 원형에서 벗어나는 모습이 보인다. 예측 성능이 떨어진다는 말이지.
tree의 수가 떨어지니까 당연하다.
blob이 n(n>1)개인 그래프에서도 원리는 같다.
| contamination=0.1 // n_estimators=100 | contamination=0.3 // n_estimators=100 |
 |
 |
| contamination=0.1 // n_estimators=5 | contamination=0.01 // n_estimators=100 |
 |
 |
그러니 기술적 측면에서 우리가 주의해야 할 요소는 contamination이 되는 셈이다.
contamination의 기준을 잡기 위해 필요한 요소들이 있다.
1. 어떤 기준으로 모델을 평가할 것인가?
- recall, precision, f1-score 등
2. 그 지표를 최대화하는 cont값은 무엇인가?
- for문을 통해 시각화하여 찾는다.
방법은 아래와 같다. 함수화하기 좋게 생겼다.
# 결과 담을 빈 리스트 선언
result = []
# range처럼 소수 범위 지정
conts = np.linspace(0.01, 0.5, 100)
# for문으로 c를 증가시키며 pred -> 결과는 result에 저장
for c in conts:
model = IsolationForest(contamination = c, random_state = 20)
model.fit(x_train)
pred = model.predict(x_val)
pred = np.where(pred == 1, 0, 1)
result.append(f1_score(y_val, pred))
print(round(max(result),3), round(conts[np.argmax(result)], 3) )
plt.plot(conts, result, marker = '.')
plt.grid()
plt.show()
c값에 따른 f1 스코어가 출력된다.
같은 원리로 한번 더 수행해서 n_estimatos도 찾을 수 있다.
result = []
for n in range(1, 95):
model = IsolationForest(contamination = 0.055, random_state = 20, n_estimators=n)
model.fit(x_train)
pred = model.predict(x_val)
pred = np.where(pred == 1, 0, 1)
result.append(f1_score(y_val, pred))
print(round(max(result),3), round(conts[np.argmax(result)], 3) )
plt.plot(range(1,95), result, marker = '.')
plt.grid()
plt.show()