
비지도학습 개요
오랜만에 Data 기반 비즈니스 문제 해결 방법론 : CRISP-DM을 보자.

1. Business Understanding : 비즈니스 문제 정의, 데이터 분석 목표 설정, ,초기 가설 수립
2. Data Understanding : 분석을 위한 구조 만들기, EDA & CDA
3. Data Preparation : 결측치 처리, 가변수화, 스케일링
4. Modeling
5. Evaluation : 기술적/비즈니스적 관점에서 평가
이중에 우리가 지금 공부하고 있는 게 모델링. 그중에서도 비지도학습니다.
모델링이란 것은 결국 데이터로부터 패턴을 찾아, 가능한 오차가 적은 수학식을 만드는 과정이다.
'가능한 오차가 적은 수학식'이라는 건, 결국 주어진 문제에 최적인 가중치(+편향)를 찾으란 거지.
이렇게 우리가 찾고자 하는 최적의 가중치와 편향을 '파라미터'라고 한다.
첫시간에도 봤듯이, 비지도학습은 Target 없이 모델을 학습시키는 모델링 방법이다.
따라서 fit 시에 x_train만 사용하고, y_train은 쓰지 않는다(애초에 없다.).
그리고 후속 작업을 해 주어야 하는데, 후속 작업의 종류는 다음과 같다.
| 차원축소 | 고차원 데이터를 축소, 시각화/지도학습으로 연계 | PCA, t-SNE |
| 클러스터링 | 자료의 군집 생성, 군집별 공통 특성 도출을 위한 추가 분석 | K-means, DBSCAN |
| 이상탐지 | 정상 데이터를 지정하여 범위 밖 데이터를 이상치로 판정 | Isolation Forest |
이것들에 대해 하나씩 알아보자.
차원 축소
차원이란 변수의 수를 말한다.
따라서 x 데이터가 3개의 열을 가지고 있다면, 3차원 데이터가 된다.
차원이 높으면(= 변수(feature)가 많으면)
(1) 모델이 복잡해진다.
(2) 데이터가 희박(sparse)해진다.
둘 다 모델의 성능을 낮추는 치명적인 요인이 된다.

특히 데이터가 희박해지면 학습이 제대로 되지 않을 가능성이 높다.
이를 '차원의 저주'라고 부른다.
이를 극복하기 위해서는 행을 늘리거나 열을 줄여 주어야 한다.
행을 늘린다는 것은 데이터를 더 많이 수집해야 한다는 것인데,
현실적으로 모델링 단계에서 이러기는 쉽지가 않다.
그렇기 때문에 우리는 열 줄이기, 즉 차원 축소를 시행한다.
고차원 데이터를 새로운 저차원 데이터로 만들자는 거지.
이때 가장 중요한 것이, 차원을 줄이되 기존 데이터의 특성을 최대한 유지해야 한다는 것이다. 욕심쟁이
이를 위한 방법이 주성분 분석(PCA)과 t-SNE이다.
PCA는 차원 m개를 n개까지 줄이는 대표적인 방법이다.
일단 2차원을 1차원으로 만드는 과정을 통해 개념을 잡아 보자.

인간 눈에도 회귀선이 보이는 2차원 데이터이다.
이 데이터를 가장 잘 설명하면서, 더 저차원인 것은 무엇일까?
회귀선이겠지. 1차원이니까. 저 회귀선이 만들어지는 과정을 잘 생각해 보자.

이 모델의 차원을 낮추는 가장 좋은 방법은,
위 그림처럼 회귀선을 찾은 후 각 벡터들을 투영하는 것이다.
벡터들이 다 지워지면 회귀선만 남을 테니까.
2차원 데이터가, 자신을 가장 잘 반영하는 1차원 데이터로 낮아진 것이다.
그런데... 저, 편의상 회귀선이라고 한,
'데이터를 가장 잘 설명하는 선'을 어떻게 찾지?
사실 우리는 이미 데이터의 방향성을 나타내는 지표를 안다.
데이터의 방향성이 잘 드러난다 = 데이터가 잘 벌어져 있다. = 분산이 크다.
데이터를 저차원으로 투영하는 원리가 드러나는 영상.
보다시피 데이터의 특성이 가장 잘 드러나는 것은 분산이 가장 큰 방향으로 그은 축이다.
이게 다차원으로 넘어가면 어떻게 될까?
위와 같은 방법으로 축을 그은 후,
그 축에 직교하는 축들 중 가장 분산이 큰 방향으로 축을 긋는다.
이를 n회 반복한다.
이 과정에서 다중공선성도 해결되는데,
다중공선성은 두 강한 상관관계에 의해 발생하지만
x에 직교하는 y란 서로 독립적인 관계이기 때문이다.
자, 그럼 코드로 PCA를 구현해 보자.
우선 PCA는 분산 비교를 기반으로 하기 때문에,
'거리 계산'이 들어가는 알고리즘이다.
그렇단건? 스케일링이 필요하다는거지.
스케일링 된 데이터를 기준으로,
PCA는 sklearn.decomposition에 있는 PCA 모듈을 통해 진행할 수 있다.
from sklearn.decomposition import PCA
# 주성분 수 2개로 PCA 선언
pca = PCA(n_components = 2)
# PCA 실행
x2_pc = pca.fit_transform(x2)
오... scaler 쓰는 방법이랑 똑같다.
만약 train과 valid 데이터가 분리되어 있는 상황이라면,
scaler 때와 마찬가지로 valid에는 transform을 사용하면 된다.
그러면 우리가 n_components의 값을 어떻게 정의해야 하는지를 생각해 보자.
차원 축소 결과물의 최대 차원 수는? 원본 차원 수와 동일하겠지(축소된 차원 0개).
n_components를 데이터의 컬럼 수만큼으로 설정하면 이렇게 될 것이다.
차원을 축소하는데 원본 수만큼 하면 안 줄어들지 않냐고?
차원 축소는 n을 최댓값으로 설정하고, 거기서 슬라이싱으로 잘라서 진행한다.
# 주성분을 몇개로 할지 결정(최댓값 : 전체 feature 수)
n = x_train.shape[1]
# 주성분 분석 선언
pca = PCA(n_components=n)
# 만들고, 적용하기
x_train_pc = pca.fit_transform(x_train)
x_val_pc = pca.transform(x_val)
# 주성분을 몇개로 할지 결정(최대값 : 전체 feature 수)
n = x_train.shape[1]
# 주성분 분석 선언
pca = PCA(n_components=n)
# 만들고, 적용하기
x_train_pc = pca.fit_transform(x_train)
x_val_pc = pca.transform(x_val)
이렇게 n_component 값을 x_train.shape[1]만큼, 즉 열의 개수만큼 주면,
열의 개수만큼 PCA가 실행된다.
재미있는 점은, n_component 값을 얼마로 주든 축이 그어지는 순서는 같다는 점이다.
예를 들어, n_component = 30으로 수행한 pca 데이터(pca30)의 첫 열은
n_component = 1로 수행한 결과(pca01)와 같다.
즉, pca30[:1] = pca01이다.
그래서, 아까 말했듯이 슬라이싱으로 잘라다 쓰면 된다.
그러므로 우리가 pca를 실제로 수행하는건 한 번으로 족하다.
그렇다면 몇개를 슬라이싱할지,
즉, 적절한 주성분의 개수는 어떻게 알 수 있을까?
이것은 pca 모듈의 'explained_variance_ratio_' 속성을 시각화하면 된다.
이 속성은 오차율을 말하는 것인데, 당연히 오차율이 낮아야 하겠지.
앞에서 데이터 전체 개수만큼 pca를 수행한 데는 이 이유도 있다.
plt.plot(range(1,n+1), pca.explained_variance_ratio_, marker = '.')
plt.xlabel('No. of PC')
plt.grid()
plt.show()
y축이 의미하는 바가 'explained_variance_ratio_'.
즉 차원 축소 없는 데이터와의 오차다.
그래프를 보면 차원이 3개만 넘어가도 오차가 확 줄어드는 것을 볼 수 있다.
자, 그럼 여기서 어떤 횟수를 고르는 게 좋을까?
이 때 사용하는 방법을 Elbow Method라고 한다.
어려운 개념은 아니고, '팔꿈치에 있는 값으로 정해라' 이런거지.
위 그래프 기준으로는 7쯤이 되겠다.

t-SNE
PCA는 거리 기반이기 때문에 실제 관계성을 반영하지 못하는 경우가 있다.
따라서 분산뿐만 아니라 다른 요소까지 고려하여
원본 데이터에서 유사도를 계산한 후 유사도 맵을 작성하는 방식으로 차원 축소를 할 수도 있다.
이 방법을 t-SNE라고 한다.
다만 이 방법은 많은 feature를 만들어낼 수는 없고, 2~3차원으로만 줄일 수 있다.
from sklearn.manifold import TSNE
# 2차원으로 축소하기
tsne = TSNE(n_components = 2, random_state=20)
x_tsne = tsne.fit_transform(x)
사용법은 PCA와 똑같다.
뭐, 3차원까지라는 제한이 있긴 하지만, 쓸 수만 있다면 아주 강력한 녀석이다.


클러스터링

클러스터링(Clustering, 군집화)의 방법으로는 K-means와 DBSCAN이 있다.
특히나 k-means의 원리를 잘 알아야 하는데, 기본적으로는 다음과 같다.
1. K값 설정: 먼저, 몇 개의 클러스터로 나눌지 결정한다. 이때의 K는 클러스터의 개수이다.
2. 초기 중심점 설정: K개의 클러스터 중심점을 무작위로 선택한다. 이 중심점들은 각 클러스터의 중심 역할을 한다.
3. 거리 계산 및 할당: 각 데이터들과 중심점 사이의 거리를 계산하고, 가장 가까운 중심점에 해당하는 클러스터에 데이터를 할당한다.
4. 중심점 재계산: 각 클러스터에 할당된 데이터 포인트들의 평균을 구해 새로운 중심점을 계산한다.
5. 반복: 중심점이 더 이상 변하지 않거나 특정 반복 횟수에 도달할 때까지 3~4단계를 반복한다.

보다시피 시각화가 중요하므로, 함수로 묶어 쓴다.
비지도학습이므로 x_train만 쓰면 된다.
def k_means_plot(x, y, k) :
# 모델 생성
model = KMeans(n_clusters= k, n_init = 'auto')
model.fit(x)
pred = model.predict(x)
# 군집 결과와 원본 데이터 합치기(concat)
pred = pd.DataFrame(pred, columns = ['predicted'])
result = pd.concat([x, pred, y], axis = 1)
# 중앙(평균) 값 뽑기
centers = pd.DataFrame(model.cluster_centers_, columns=['x1','x2'])
# 그래프 그리기
plt.figure(figsize = (8,6))
plt.scatter(result['x1'],result['x2'],c=result['predicted'],alpha=0.5)
plt.scatter(centers['x1'], centers['x2'], s=50,marker='D',c='r')
plt.grid()
plt.show()| k_means_plot(x, y, k = 2) | k_means_plot(x, y, k = 4) |
 |
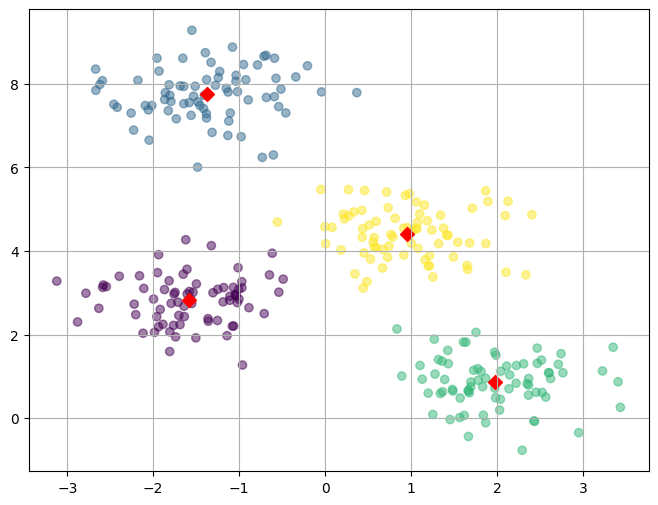 |
일련의 과정들을 쭉 보아하니, 클러스터 수 k를 어떻게 지정하는지가 가장 중요해 보인다.
어떻게 정해야 할까?
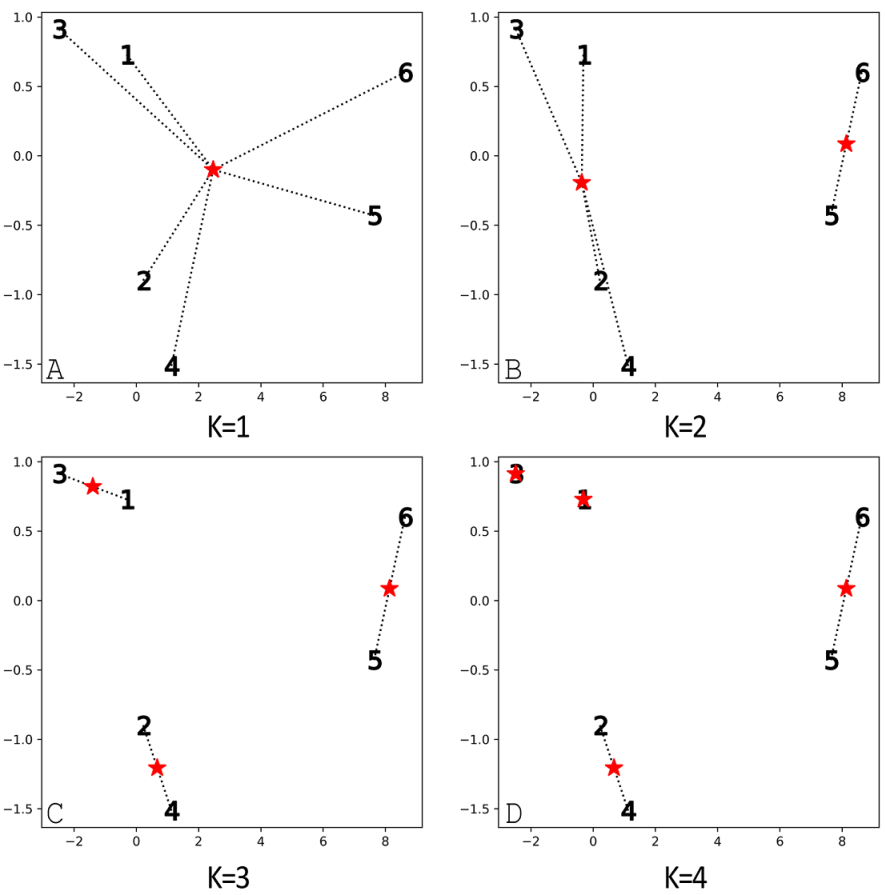
Inertia Value는 각 중심점에서 각 데이터까지의 거리의 합을 뜻한다.
위 그림에서 보이듯이, 이 값은 k=1일 때 가장 크다.
Inertai Value와 성능의 관계를 알아보자.
# k를 증가시키면서 inertia value를 저장
kvalues = range(1, 10)
inertias = []
for k in kvalues:
model = KMeans(n_clusters=k, n_init = 'auto')
model.fit(x)
inertias.append(model.inertia_)
# 시각화
plt.figure(figsize = (8, 6))
plt.plot(kvalues, inertias, marker='o')
plt.xlabel('number of clusters, k')
plt.ylabel('inertia')
plt.grid()
plt.show()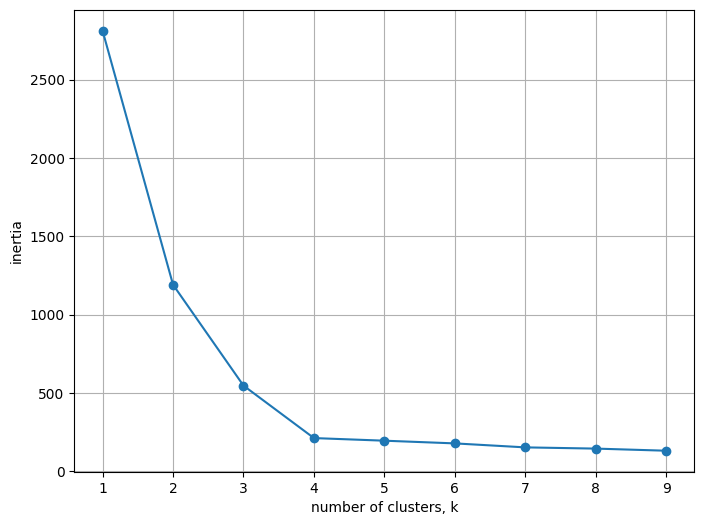
이렇게 k값에 따른 Inertia Value를 시각화해 보면,
꺾이는 지점에서 Elbow Method로 k값을 선택할 수 있다.(k = 4)
또는 실루엣 점수를 찾는 방법도 있다.
sklearn의 metrics 패밀리에 속한 실루엣 점수는 -1 ~ 1사이에서 책정되는데
1에 가깝다는 것은 클러스터 간의 거리는 멀고, 클러스터 내부의 거리는 가깝다는 뜻이다.
따라서 실루엣 점수는 1에 가까울수록 품질이 좋다.
# 실루엣 점수 임포트
from sklearn.metrics import silhouette_score
# 클러스터 개수에 따른 실루엣 점수를 저장할 리스트
kvalues = range(2, 10) # 최소 2개 이상이어야 함.
sil_score = []
for k in kvalues:
# KMeans 모델 생성
model = KMeans(n_clusters=k, n_init = 'auto')
# 모델을 학습하고 예측
pred = model.fit_predict(x)
# 실루엣 점수 계산
sil_score.append(silhouette_score(x, pred))
# 실루엣 점수 시각화
plt.figure(figsize = (8, 6))
plt.plot(kvalues, sil_score, marker='o')
plt.xlabel('n_clusters')
plt.ylabel('Silhouette Score')
plt.grid()
plt.show()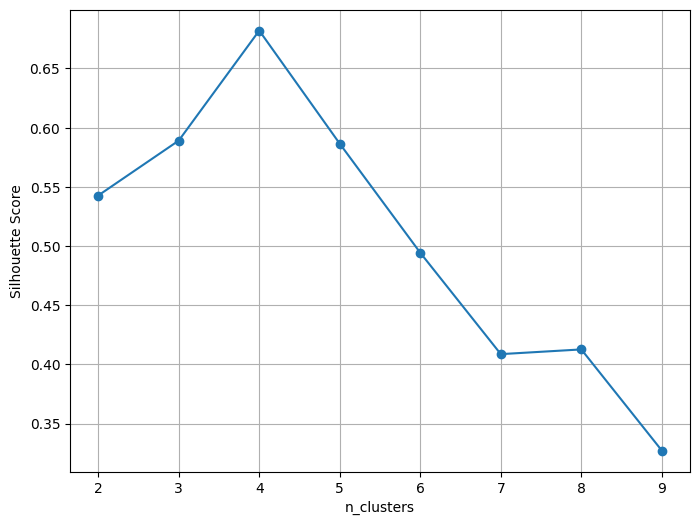
실루엣 점수가 4에서 가장 높다.
다만 이렇게 실루엣 점수와 Inertia Value가 일치할 수도, 그렇지 않을 수도 있다는 것을 유념해야 한다.
그럼 이 두가지를 동시에 활용할 수 있는 코드블록을 만들어 보자.
# x 데이터에 대한 스케일링
scaler = MinMaxScaler()
x_s = scaler.fit_transform(x)
# 모델 생성
kvalue = range(2, 21)
inertia = []
sil_score = []
for k in kvalue:
model = KMeans(n_clusters=k, n_init='auto')
model.fit(x_s)
pred = model.predict(x_s)
inertia.append(model.inertia_)
sil_score.append(silhouette_score(x_s, pred))
# 시각화
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(kvalue, inertia, marker='o')
plt.xlabel('K-value')
plt.ylabel('Inertia')
plt.subplot(1, 2, 2)
plt.plot(kvalue, sil_score, marker='o')
plt.xlabel('K-value')
plt.ylabel('Silhouette')
plt.grid(lw=0.3)
plt.tight_layout()
plt.show()
보아하니 k=6이나 k=8정도가 적절해 보인다.